简介

期望最大化(ExpectationMaximization)算法最初是由 Ceppellini[2]等人1950年在讨论基因频率的估计的时候提出的。后来又被Hartley[3]和Baum[4]等人发展的更加广泛。目前引用的较多的是1977年Dempster[5]等人的工作。它主要用于从不完整数据中计算最大似然估计。后来经过其他学者的发展，这个算法也被用于聚类等应用。

最大似然估计

重复强调下，EM算法主要用于从不完整数据中计算最大似然估计，本身可以看成是特殊情况下计算极大似然的一种方法。

极大似然估计是要解决这样一个问题：给定一组数据和一个参数待定的模型，如何确定模型的参数，使得这个确定参数后的模型在所有模型中产生已知数据的概率最大。（模型已定，参数未知）

我们通过一个抛硬币的实验和体会下算法的思想。

考虑一个投掷硬币的实验：现在我们有两枚硬币 $ A $ 和 $ B $ ，这两枚硬币和普通的硬币不一样，他们投掷出正面的概率和投掷出反面的概率不一定相同。我们将 $ A $ 和 $ B $ 投掷出正面的概率分别记为 $ \theta_A $ 和 $ \theta_B $ 。现在独立地做5次试验：随机的从这两枚硬币中抽取1 枚，投掷10次，统计出现正面的次数。将结果整理为如下的表格：

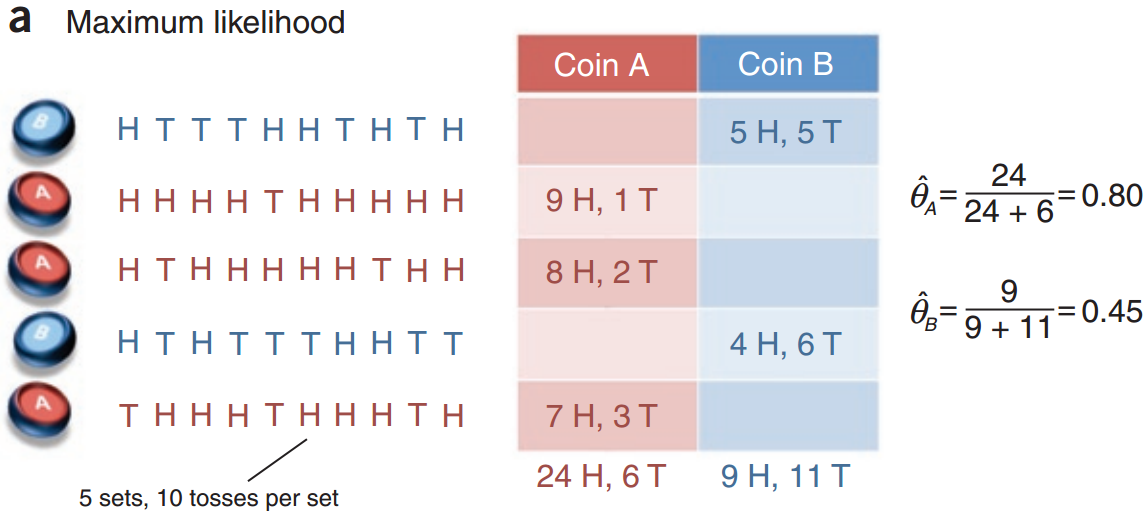
我们记录下两组随机变量 $ X = (X_1,X_2,X_3,X_4,X_5) $ 和 $ Z =(Z_1,Z_2,Z_3,Z_4,Z_5) $ ，其中 $ X_i\in \{0,1,2,3,4,5,6,7,8,9,10\} $ 代表试验 $ i $ 中出现 正面的次数， $Z_i \in \{A,B\}$ 代表这次试验投掷的是硬币 $ A $ 还是硬币 $ B $ 。

我们的目标是根据实验结果来估计参数 $ \theta =(\theta_A,\theta_B) $ 。这个实验中的参数估计就是有完整数据的参数估计，这个是因为我们不仅知道每次试验中投掷出正面的次数，我们还知道每次试验中投掷的是硬币 $ A $ 还是 $ B $ 。

$$\begin{aligned} L(\theta) & = P(X,Z|\theta)\\ & = C_5^3P(Z=A)^3(1-P(Z=A))^2\\ & C_{10}^5\theta_B^5(1-\theta_B)^5C_{10}^9\theta_A^9(1-\theta_A)\notag \\ & C_{10}^8\theta_A^8(1-\theta_A)^2C_{10}^4\theta_B^4(1-\theta_B)^6C_{10}^7\theta_A^7(1-\theta_A)^3\notag\end{aligned}$$

而， $ \hat{\theta} = \arg\max\limits_{\theta} L(\theta) $ ，易求得， $ \hat{\theta}_A = 0.8,\hat{\theta}_B = 0.45 $ 。这就是我们一直所熟知的极大似然估计。

EM算法

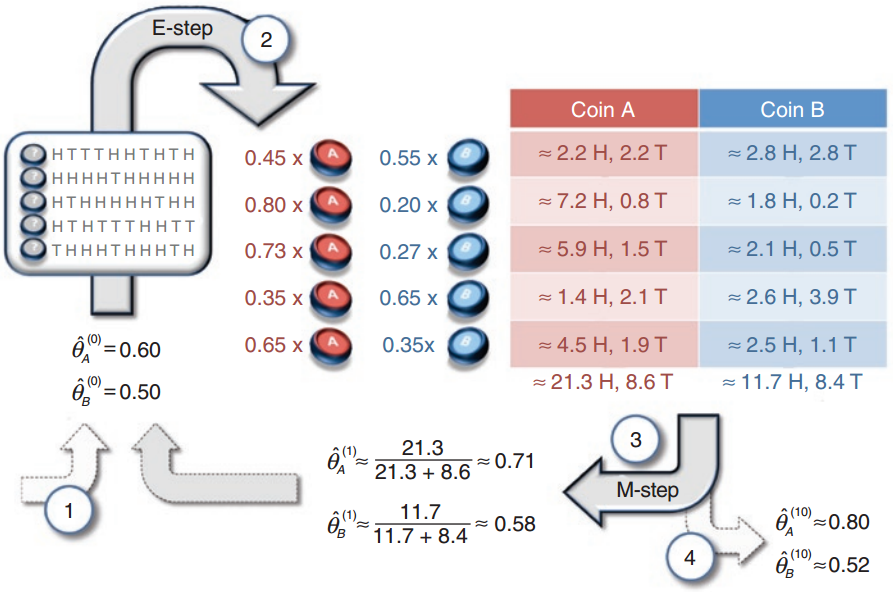
我们将这个问题稍微改变一下：假设我们现在只知道每次试验有几次投掷出正面，但是不知道每次试验投掷的是哪枚硬币。这个时候我们就称 $ Z $ 为(Hidden Variable)， $ X $ 称为观察变量(Observed Variable)。当我们再来估计参数 $ \theta_A $ 和 $ \theta_B $ 时，数据就不够完整了。传统的极大似然估计很难解决，轮到EM算法上台展现了。

怎么玩呢？

一个基本的思路是：

1. 首先我们给 $ \theta $ 赋一组初始值。（初始值我们可以通过经验或专门的算法得到，这里不做展开）

   $$\hat{\theta}_A^{(0)} = 0.60, \hat{\theta}_B^{(0)} = 0.50$$

2. 然后基于这组 $ \theta $ 值估计每一次实验更有可能抛的哪一枚硬币。

   比如第一次试验中，如果投掷的是 $ A $ ，那么出现5个正面的概率为: $C_{10}^5 0.6^5(1-0.6)^5 = 0.20$ 如果投掷的是 $ B $ ，那么相应的概率为:

   $$C_{10}^5 0.5^5(1-0.5)^5 = 0.2460$$

   也就是掷 $ B $ 的概率高于 $ A $ ，我们可以判定第一次掷的是 $ B $ .

   其他的几组采用同样的计算方法，最后得到的结果是 $ (B,A,A,B,A) $ ¹。

3. 上一步中我们相当于得到了隐藏变量 $ Z $ 的分布，此时问题就变为了我们上一节的问题（）。通过求导我们可得出 $ \theta_{n+1} $ 。

4. 重复以上步骤，直至 $ \theta $ 收敛。

EM算法的大致思路便是如此，只是在第二步处理上有所不同。它在估计每次实验所抛硬币时，并不直接判定这次抛就是硬币 $ A $ 或者 $ B $ ，而是计算出 是 $ A $ 或是 $ B $ 的概率（也就是 $ Z $ 的分布）；在这个基础上计算似然函数。本篇的最后我们会详细演示计算细节。通俗地总结下²：

简版：猜（E-step）,反思（M-step）,重复；
啰嗦版：你知道一些东西（观察的到的数据），你不知道一些东西（隐藏变量），你很好奇，想知道点那些不了解的东西。怎么办呢？
你根据一些假设（parameter）先猜（E-step），把那些不知道的东西都猜出来，假装你全都知道了;
然后有了这些猜出来的数据，你反思一下，更新一下你的假设（parameter）,
让你观察到的数据更加可能(Maximize likelihood; M-step);
然后再猜，再反思，最后，你就得到了一个可以解释整个数据的假设了。

那么为什么这种方法行得通呢？有没有失效的时候呢？迭代是否一定会收敛呢？这就需要严格的数学证明了。

EM算法推导

我们先写出似然函数表达式，：

$$\begin{aligned} L(\theta) & = \ln \mathcal{P}(\textbf{X}|\theta)\\ \mathcal{P}(\textbf{X}|\theta)& = \sum\limits_{\textbf{z}} \mathcal{P}(\textbf{X}|\textbf{z},\theta)\mathcal{P}(\textbf{z}|\theta)\end{aligned}$$

由于隐藏变量的存在，我们无法像最大似然估计,那样通过求偏导那一套方法来估计参数 $ \theta $ .

EM算法采用迭代的方法估计参数，保证每一次估计值都比上一次更加接近真实值，这就要求 $ L(\theta) $ 每一次迭代过程中都要递增。我们假设第 $ n $ 次迭代 $ \theta $ 的估计值为 $ \theta^n $ ，第 $ n+1 $ 次迭代时，

$$L(\theta) - L(\theta^n) = \ln \mathcal{P}(\textbf{X}|\theta) - \ln \mathcal{P}(\textbf{X}|\theta^n)$$

我们希望最大化这个差值，这样我们就能不断逼近 $ L(\theta) $ 的最大值。我们来变换下这个式子，

$$\begin{aligned} L(\theta) - L(\theta^n) & = \ln \mathcal{P}(\textbf{X}|\theta) - \ln \mathcal{P}(\textbf{X}|\theta^n) \notag\\ & = \ln \sum\limits_{\textbf{z}} \mathcal{P}(\textbf{X}|\textbf{z},\theta)\mathcal{P}(\textbf{z}|\theta) - \ln \mathcal{P}(\textbf{X}|\theta^n)\notag\\ & = \ln \sum\limits_{\textbf{z}} \mathcal{P}(\textbf{X}|\textbf{z},\theta)\mathcal{P}(\textbf{z}|\theta)\cdot \frac{\mathcal{P}(\textbf{z}|\textbf{X},\theta^n)}{\mathcal{P}(\textbf{z}|\textbf{X},\theta^n)} - \ln \mathcal{P}(\textbf{X}|\theta^n)\notag\\ & = \underbrace{\ln \sum\limits_{\textbf{z}} \mathcal{P}(\textbf{z}|\textbf{X},\theta^n)\left(\frac{\mathcal{P}(\textbf{X}|\textbf{z},\theta)\mathcal{P}(\textbf{z}|\theta)}{\mathcal{P}(\textbf{z}|\textbf{X},\theta^n)}\right)} - \ln \mathcal{P}(\textbf{X}|\theta^n) \label{em1}\end{aligned}$$

这个时候我们需要利用下著名的Jensen不等式³：

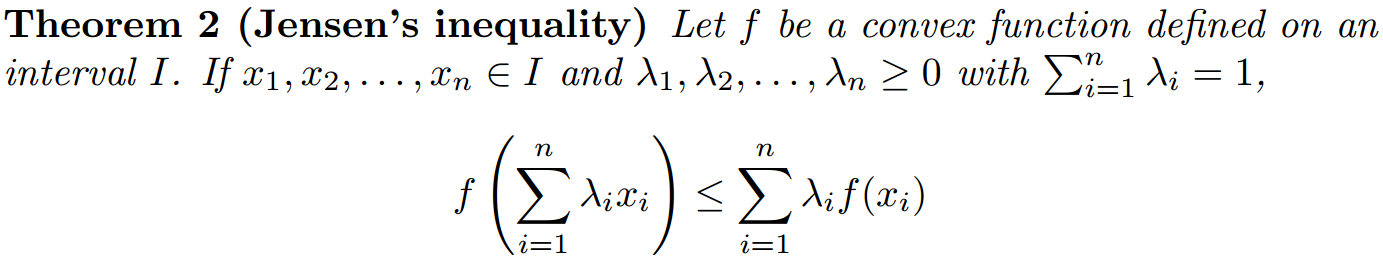
因为 $ \ln(x) $ 为严格的单调递增函数，根据Jensen不等式，有，

$$\label{em2} \ln \sum\limits_{i=1}^n \lambda_i x_i \geq \sum\limits_{i=1}^n \ln(x_i)$$

又因为，

$$\begin{aligned} \sum\limits_{\textbf{z}} \mathcal{P}(\textbf{z}|\textbf{X},\theta^n) & = 1\\ \mathcal{P}(\textbf{z}|\textbf{X},\theta^n) & \geq 0\end{aligned}$$

我们要化简的是式[em1]，这个时候可以将 $ \mathcal{P}(\textbf{z}|\textbf{X},\theta^n) $ 看做式[em2]中的 $ \lambda_i $ ，$\frac{\mathcal{P}(\textbf{X}|\textbf{z},\theta)\mathcal{P}(\textbf{z}|\theta)}{\mathcal{P}(\textbf{z}|\textbf{X},\theta^n)} $ 看做式[em2]中的 $ x_i $ ，则有：

$$\begin{aligned} L(\theta) - L(\theta^n) &= \ln \sum\limits_{\textbf{z}} \mathcal{P}(\textbf{z}|\textbf{X},\theta^n)\left(\frac{\mathcal{P}(\textbf{X}|\textbf{z},\theta)\mathcal{P}(\textbf{z}|\theta)}{\mathcal{P}(\textbf{z}|\textbf{X},\theta^n)}\right) - \ln \mathcal{P}(\textbf{X}|\theta^n) \notag\\ & \geq \sum\limits_{\textbf{z}} \mathcal{P}(\textbf{z}|\textbf{X},\theta^n) \ln \left(\frac{\mathcal{P}(\textbf{X}|\textbf{z},\theta)\mathcal{P}(\textbf{z}|\theta)}{\mathcal{P}(\textbf{z}|\textbf{X},\theta^n)}\right) - \ln \mathcal{P}(\textbf{X}|\theta^n) \notag\\ & = \sum\limits_{\textbf{z}} \mathcal{P}(\textbf{z}|\textbf{X},\theta^n) \ln \left(\frac{\mathcal{P}(\textbf{X}|\textbf{z},\theta)\mathcal{P}(\textbf{z}|\theta)}{\mathcal{P}(\textbf{z}|\textbf{X},\theta^n)}\right) - \sum\limits_{\textbf{z}} \mathcal{P}(\textbf{z}|\textbf{X},\theta^n)\ln \mathcal{P}(\textbf{X}|\theta^n) \notag\\ & = \sum\limits_{\textbf{z}} \mathcal{P}(\textbf{z}|\textbf{X},\theta^n) \ln \left(\frac{\mathcal{P}(\textbf{X}|\textbf{z},\theta)\mathcal{P}(\textbf{z}|\theta)}{\mathcal{P}(\textbf{z}|\textbf{X},\theta^n)\mathcal{P}(\textbf{X}|\theta^n)}\right) \notag\\ & \triangleq \Delta (\theta|\theta^n)\end{aligned}$$

也就是说，

$$L(\theta) \geq L(\theta^n) + \Delta (\theta|\theta^n)$$

不妨令，

$$l(\theta|\theta^n) \triangleq L(\theta^n) + \Delta (\theta|\theta^n)$$ $$L(\theta) \geq l(\theta|\theta^n)$$

而又有,

$$\begin{aligned} l(\theta^n|\theta^n) & = L(\theta^n) + \Delta (\theta^n|\theta^n) \\ & = L(\theta^n) + \sum\limits_{\textbf{z}} \mathcal{P}(\textbf{z}|\textbf{X},\theta^n) \ln \frac{\mathcal{P}(\textbf{X}|\textbf{z},\theta^n)\mathcal{P}(\textbf{z}|\theta^n)}{\mathcal{P}(\textbf{z}|\textbf{X},\theta^n)\mathcal{P}(\textbf{X}|\theta^n)}\\ & = L(\theta^n) + \sum\limits_{\textbf{z}} \mathcal{P}(\textbf{z}|\textbf{X},\theta^n) \ln \frac{\mathcal{P}(\textbf{X},\textbf{z}|\theta^n)}{\mathcal{P}(\textbf{X},\textbf{z}|\theta^n)}\\ & = L(\theta^n) + \sum\limits_{\textbf{z}} \mathcal{P}(\textbf{z}|\textbf{X},\theta^n) \ln 1 \\ & = L(\theta^n)\end{aligned}$$

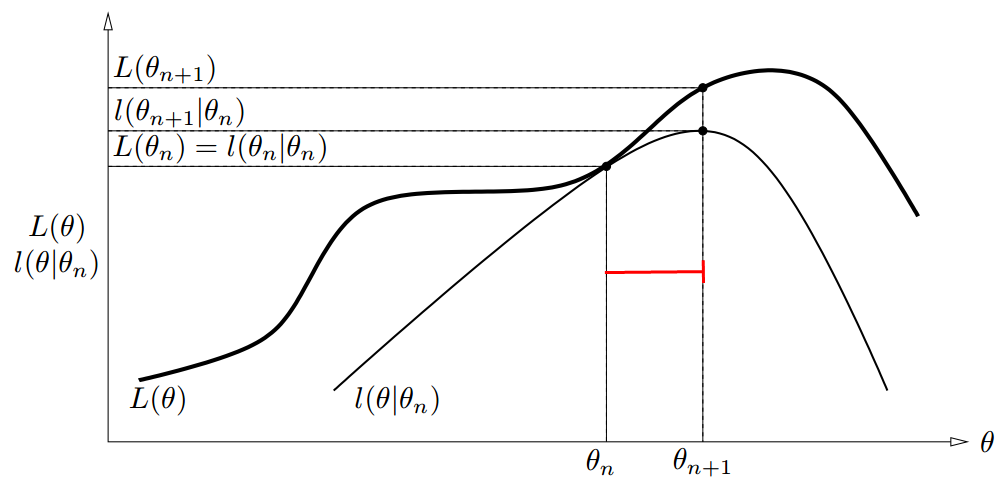
上面推导了那么多，其实都是为了得出这张图。由 $L(\theta) \geq l(\theta|\theta^n)$ ， $ L(\theta) $ 为 $ l(\theta|\theta^n) $ 的上边界。又因为 $ l(\theta^n|\theta^n) = L(\theta^n) $，我们知道 $ L(\theta) $ 和 $ l(\theta|\theta^n) $ 在 $ \theta = \theta^n $ 时相等。通过令 $ \theta^{n+1} = \arg \max\limits_{\theta} l(\theta^n|\theta^n) $ ，我们保证了 $ L(\theta) $ 的值在每一步迭代过程中都是增加的。

我们进一步推导下，

$$\begin{aligned} \theta^{n+1} & = \arg \max\limits_{\theta} l(\theta^n|\theta^n)\\ & = \arg \max\limits_{\theta} \left \{ \sum\limits_{\textbf{z}} \mathcal{P}(\textbf{z}|\textbf{X},\theta^n) \ln \frac{\mathcal{P}(\textbf{X}|\textbf{z},\theta)\mathcal{P}(\textbf{z}|\theta)}{\mathcal{P}(\textbf{z}|\textbf{X},\theta^n)\mathcal{P}(\textbf{X}|\theta^n)} \right \} \\ & = \arg \max\limits_{\theta} \left \{ \sum\limits_{\textbf{z}} \mathcal{P}(\textbf{z}|\textbf{X},\theta^n) \ln \mathcal{P}(\textbf{X}|\textbf{z},\theta)\mathcal{P}(\textbf{z}|\theta) \right \} \\ & = \arg \max\limits_{\theta} \left \{ \sum\limits_{\textbf{z}} \mathcal{P}(\textbf{z}|\textbf{X},\theta^n) \ln \frac{\mathcal{P}(\textbf{X},\textbf{z},\theta)}{\mathcal{P}(\textbf{z},\theta)}\frac{\mathcal{P}(\textbf{z},\theta)}{\mathcal{P}(\theta)} \right \}\\ & = \arg \max\limits_{\theta} \left \{ \sum\limits_{\textbf{z}} \mathcal{P}(\textbf{z}|\textbf{X},\theta^n) \ln \mathcal{P}(\textbf{X},\textbf{z}|\theta) \right \}\\ & = \underbrace{\arg \max\limits_{\theta}}_{M-step} \underbrace{\vphantom{\arg \max\limits_{\theta}}\left \{ E_{\textbf{z}|\textbf{X},\theta_n}\{ \ln \mathcal{P} (\textbf{X},\textbf{z}|\theta) \}\right \}}_{E-step}\end{aligned}$$

推导至此，EM算法的框架就已经十分清晰了，包含两大步骤： 1. 计算期望： $ E_{\textbf{z}|\textbf{X},\theta_n}{ \ln \mathcal{P} (\textbf{X},\textbf{z}|\theta)} $ 2. 求得使期望最大化的 $ \theta $

EM算法收敛性

通过前面的证明，我们很容易得到：

$$\Delta (\theta^{n+1}|\theta^n) \geq \Delta (\theta^n|\theta^n) = 0$$

这保证了EM算法每一次迭代中， $ L(\theta) $ 都是非减的。但如果 $ \theta_n $ 正好是函数 $l(\theta|\theta^n)$ 的极大值点呢？此时 $\theta^{n+1} = \arg \max\limits_{\theta} l(\theta|\theta^n) = \theta_n$ ，迭代终止，算法有可能陷入局部最大值，而得不到全局最优。

例子演算

下面我们重新回顾下Section [section:example]中的例子，

• 计算期望：$ E_{\textbf{z}|\textbf{X},\theta_n}{ \ln \mathcal{P} (\textbf{X},\textbf{z}|\theta)} $ ； 可以分为两部分: $ \mathcal{P}(\textbf{z}|\textbf{X},\theta^n) $ 和 $ \mathcal{P} (\textbf{X},\textbf{z}|\theta) $

$$\begin{aligned} \mathcal{P}(\textbf{z}|\textbf{X},\theta^n) & = \mathcal{P}(\textbf{z}_1,\textbf{z}_2,\textbf{z}_3,\textbf{z}_4,\textbf{z}_5|\textbf{X}_1,\textbf{X}_2,\textbf{X}_3,\textbf{X}_4,\textbf{X}_5,\theta^n)\\ \mathcal{P}(\textbf{z}_i|\textbf{X}_i,\theta^n) & = \frac{\mathcal{P}(\textbf{X}_i|\textbf{z}_i,\theta^n)\mathcal{P}(\textbf{z}_i|\theta^n)}{\mathcal{P}(\textbf{X}_i|\theta^n)}\\ & = \frac{\mathcal{P}(\textbf{X}_i|\textbf{z}_i,\theta^n)\mathcal{P}(\textbf{z}_i)}{\sum\limits_{\textbf{z}_i} \mathcal{P}(\textbf{X}_i|\theta^n)}\\ & = \frac{(\theta_{z_i}^n)^{H_i}(1-\theta_{z_i}^n)^{T_i}}{\sum\limits_{\textbf{z}_i} (\theta_{z_i}^n)^{H_i}(1-\theta_{z_i}^n)^{T_i}}\ \ (z_i \in \{A,B\})\\ \mathcal{P} (\textbf{X}_i,\textbf{z}_i|\theta) & = \mathcal{P} (\textbf{X}_i|\textbf{z}_i,\theta)\mathcal{P}(\textbf{z}_i|\theta)\\ & = (\theta_{z_i})^{H_i}(1-\theta_{z_i})^{T_i} \end{aligned}$$

• 求得使期望最大化的 $ \theta $ .

---

---

---